What is the Keyring?
The Keyring is a visualization tool that shows chords and scales as shapes. These shapes stay the same across keys, inversions, and modes, so the Keyring can be a powerful way to get to know how scales and chords behave in general.
I use the Keyring in my YouTube videos, blog posts, my online course, and in The Synthase Guide to Chords.
How do you read the Keyring?
This article is great for a quick reference, and it goes into some detail about how the Keyring appears sometimes as a static image. For a demo of the Keyring with sound and animation, check out this video:
A keyboard is an alternation of black and white keys, which is most noticeable if you look at the back half of a keyboard.

Here you can see that two notes right next to each other could both be white, or they could be a mixture of white and black. Either way, this distance—the smallest distance on a piano—is called a half step.
After twelve half steps, the pattern of black and white repeats again. The distance between two notes twelve half steps apart is called an octave.
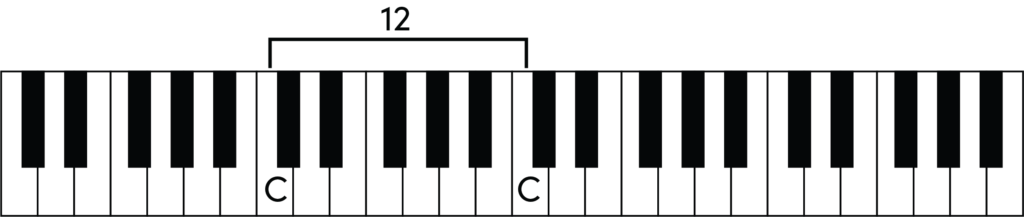
An octave is a very special relationship, and if you play two notes an octave apart, you’ll notice that there’s a way in which they sound “the same.” For that reason, we give the same names (like A, E-flat, or C-sharp) to notes that are any number of octaves apart.
Cycles that start over after twelve show up in other parts of our lives, like the months of a year or the hours on a clock. In the case of a clock, we’re used to seeing this cycle visualized as a circle. Even though time keeps moving forward, the hours start over again after twelve.
If you give the same treatment to the notes on a piano keyboard, you can wrap an octave in a circle. Even though the pitch keeps getting higher, the note names start over after twelve. I call this the Keyring, because it’s a ring of keys. Just like a clock, up is always clockwise, so it helps to always read it moving clockwise.

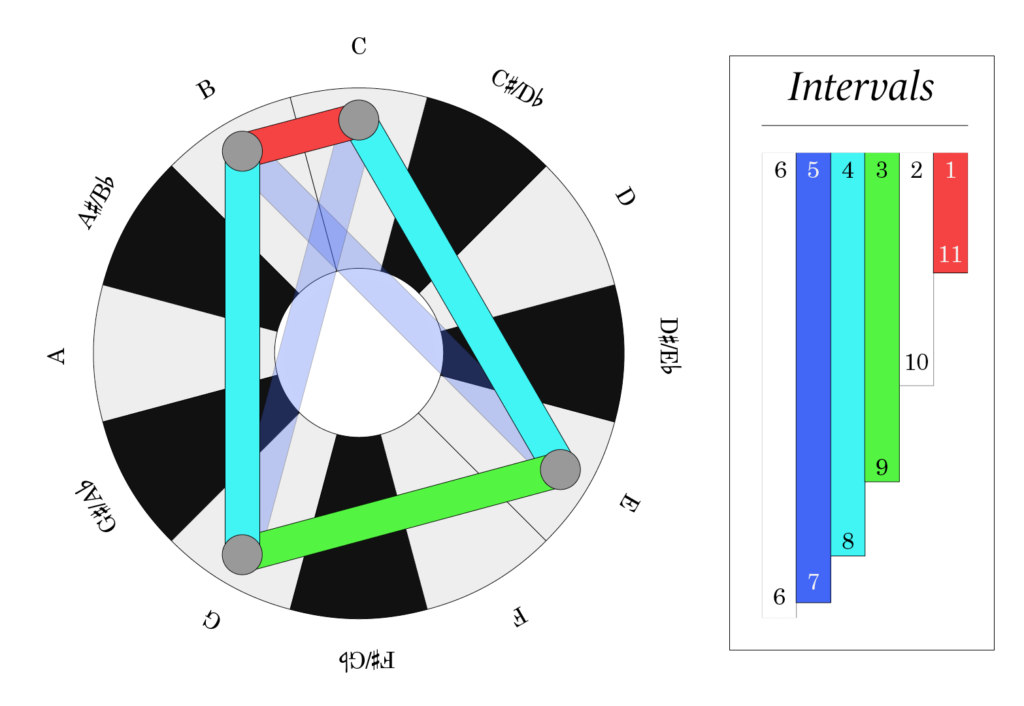
Intervals
The distance between two notes is called an interval. Since there are twelve half steps in an octave, there are eleven interval sizes smaller than an octave. The simplest way to understand these intervals is by their number of half steps: 1, 2, 3, 4, …, 11.
Two intervals that add up to an octave have a special relationship and are called complementary. It takes four half steps to go up from C to E, and eight half steps to go from that E to a higher C, so these two intervals are complementary.
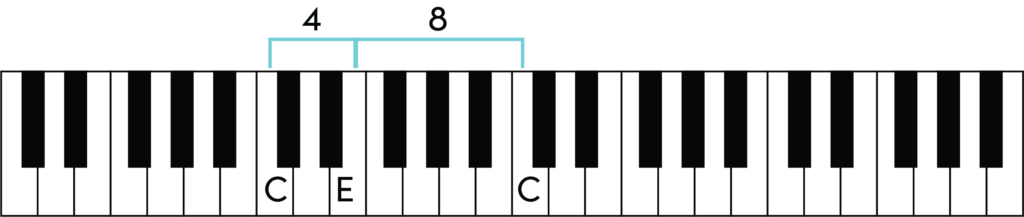
One way to tell if two intervals are complementary is by seeing if their half steps add up to twelve, since there are twelve half steps in an octave. In the above example, 4 + 8 = 12, so we’re good.
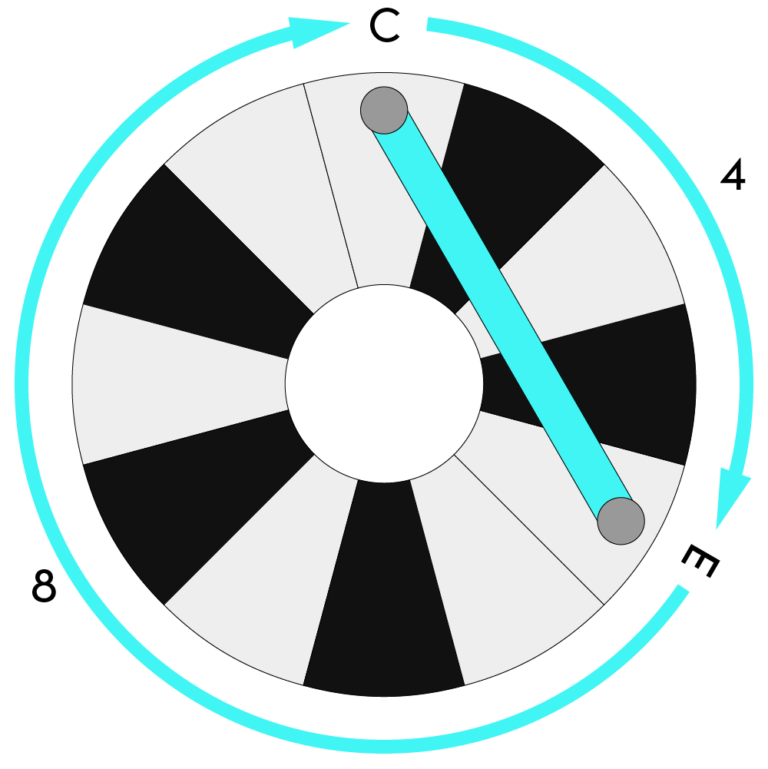
On the Keyring, complementary intervals appear the same, because depending on which one you start with, you could get either of the two intervals.
This can be a little confusing at first, but just remember that clockwise is always up, and try these things out on a keyboard, and it will start making intuitive sense.
Interval Legends
Sometimes for convenience I show the intervals contained within chords or scales in a chart like this:
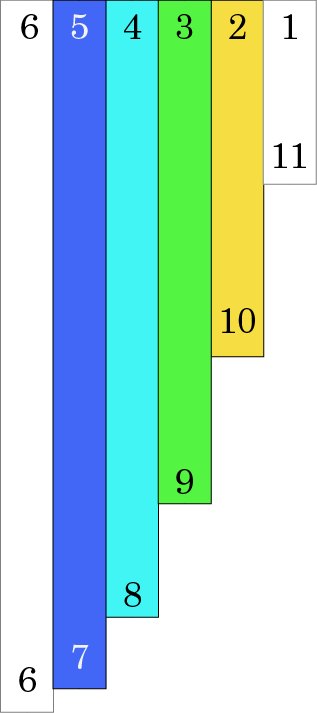
Each bar is the same length and color as an interval on the keyring (white bars are not present in the chord). The numbers on the top and bottom of the bars are the possible sizes of the interval in half steps. Notice that they add up to twelve, so these represent the two complementary intervals. It’s worth noting that there’s nothing in this legend that you couldn’t figure out just by counting half steps on the keyring: a green line connects dots that are three half steps apart, so it’s an interval size of three if you’re going the short way around, or nine if you go the long way.
In addition to having sizes measured in half steps, intervals have common names, which are related to the diatonic scale (white keys only) rather than the chromatic scale (all white and black keys). Here’s a table that will help you translate between the two systems. Each row is a pair of complementary intervals.
| Half Steps | Name | Half Steps | Name |
|---|---|---|---|
| 0 | Perfect unison | 12 | Perfect octave |
| 1 | Minor second | 11 | Major seventh |
| 2 | Major second | 10 | Minor seventh |
| 3 | Minor third | 9 | Major sixth |
| 4 | Major third | 8 | Minor sixth |
| 5 | Perfect fourth | 7 | Perfect fifth |
| 6 | Augmented fourth | 6 | Diminished fifth |


